题目描述:
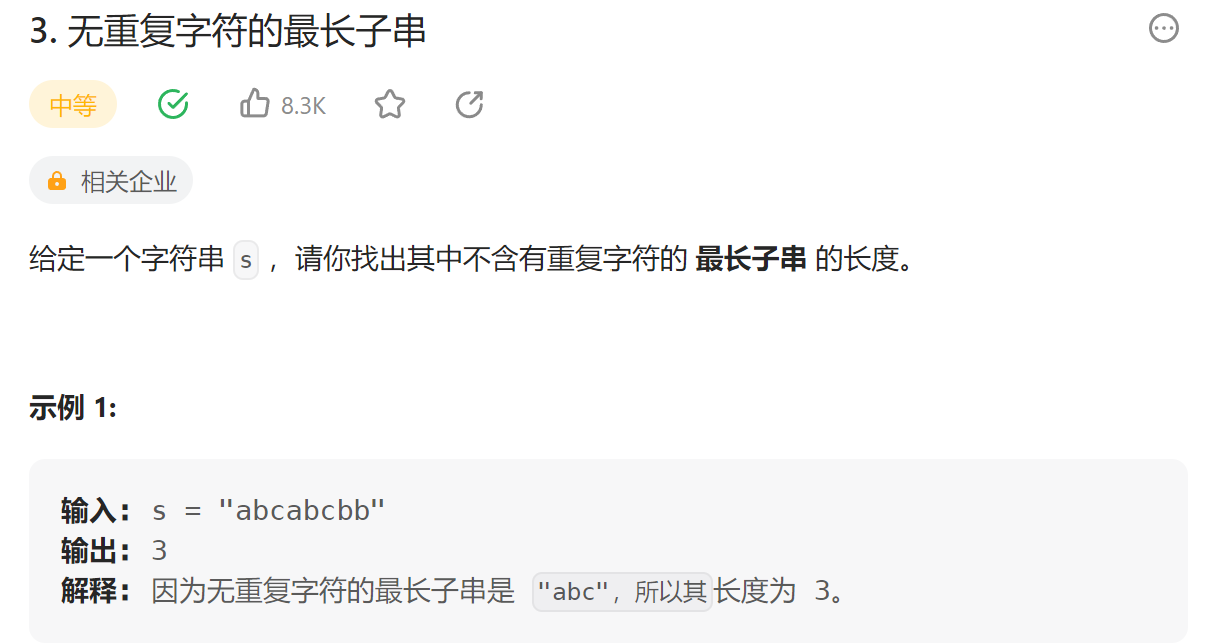
题目描述如下
题解一:
首先想到一个暴力的方法,考虑所有的子串。比如一个字符串的长度是n,那么它有1个长度为n的子串,2个长度为n-1的子串,…,n个长度为1的子串。从长到短遍历,对于每个子串判断其是否包含重复元素(这个比较简单),一旦找到长度为x的不重复的子串,就可以返回长度x了。
时间复杂度是O(n3),长度遍历一层循环、特定长度子串遍历一层循环、判断是否重复一层循环。
这个方法是正确的,但是不能ac。因为太慢了,最长的一个测试样例时间超限。
源代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public:
bool ifExist(char* arr,int count, char c){
for(int i=0;i<count;i++){
if(arr[i] == c){
return true;
}
}
return false;
}
bool ifRe(char* s, int len){
char arr[200];
int count = 0;
for(int i=0;i<len;i++){
if(ifExist(arr, count, s[i])){
return true;
}
arr[count] = s[i];
count++;
}
return false;
}
int lengthOfLongestSubstring(string s) {
int len = s.length();
for(int i=len;i>=1;i--){
int nums = len - i + 1;
for(int j=0;j<nums;j++){
char temp[50000];
for(int k=j;k<(j+i);k++){
temp[k-j] = s[k];
}
if(!ifRe(temp, i)){
return i;
}
}
}
return 0;
}
};
|
题解二:
只好选择时间复杂度更为优化的算法。
想到,遍历字符串的每个字符,所有的子串一定是以其中某个字符开头的连续序列。那么我们把每个字符开头的最长连续子串长度算出,再取其中的max即可。
对于每个字符,逐个取其后的字符,如果没有重复就加入子串,直到出现重复,从而计算出最长长度。
源代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public:
bool ifExist(char* arr,int count, char c){
for(int i=0;i<count;i++){
if(arr[i] == c){
return true;
}
}
return false;
}
int lengthOfLongestSubstring(string s) {
int len = s.length();
int* max;
max = new int[len];
for (int i = 0; i < len; i++)
{
char start = s[i];
char temp[50000];
temp[0] = start;
int maxlen = 1;
for (int j = i+1; j < len; j++)
{
if(ifExist(temp, maxlen, s[j])){
break;
}
temp[maxlen] = s[j];
maxlen += 1;
}
max[i] = maxlen;
}
int result = 0;
for (int i = 0; i < len; i++)
{
if(max[i] > result){
result = max[i];
}
}
return result;
}
};
|
这个算法已经可以通过测试了,但是时间复杂度不算好,O(n2)。
题解三:
在题解二的基础上进一步优化。
实际上题解二是有重复计算的部分的:对于第k个字符,其最长不重复子串可能到第rk个字符。那么我们继续计算k+1个字符的最长不重复子串时,k+1到rk的字符子串是不会重复的,完全可以避免判断,直接从rk之后开始。所以只需要维护一个变量last,记录上一个字符最后的索引,下一次直接从last+1开始考虑,前面照搬即可。
源代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
public:
bool ifExist(char* arr,int count, char c){
for(int i=0;i<count;i++){
if(arr[i] == c){
return true;
}
}
return false;
}
int lengthOfLongestSubstring(string s) {
int len = s.length();
int* max;
max = new int[len];
int last = 0;
for (int i = 0; i < len; i++)
{
char temp[50000];
for(int j=i;j<=last;j++){
temp[j-i] = s[j];
}
int maxlen = last - i + 1;
for (int j = last+1; j < len; j++)
{
if(ifExist(temp, maxlen, s[j])){
break;
}
temp[maxlen] = s[j];
maxlen += 1;
}
max[i] = maxlen;
last = i + maxlen - 1;
}
int result = 0;
for (int i = 0; i < len; i++)
{
if(max[i] > result){
result = max[i];
}
}
return result;
}
};
|
虽然时间复杂度还是O(n2),但是一定比上一个方法快。
以上。




